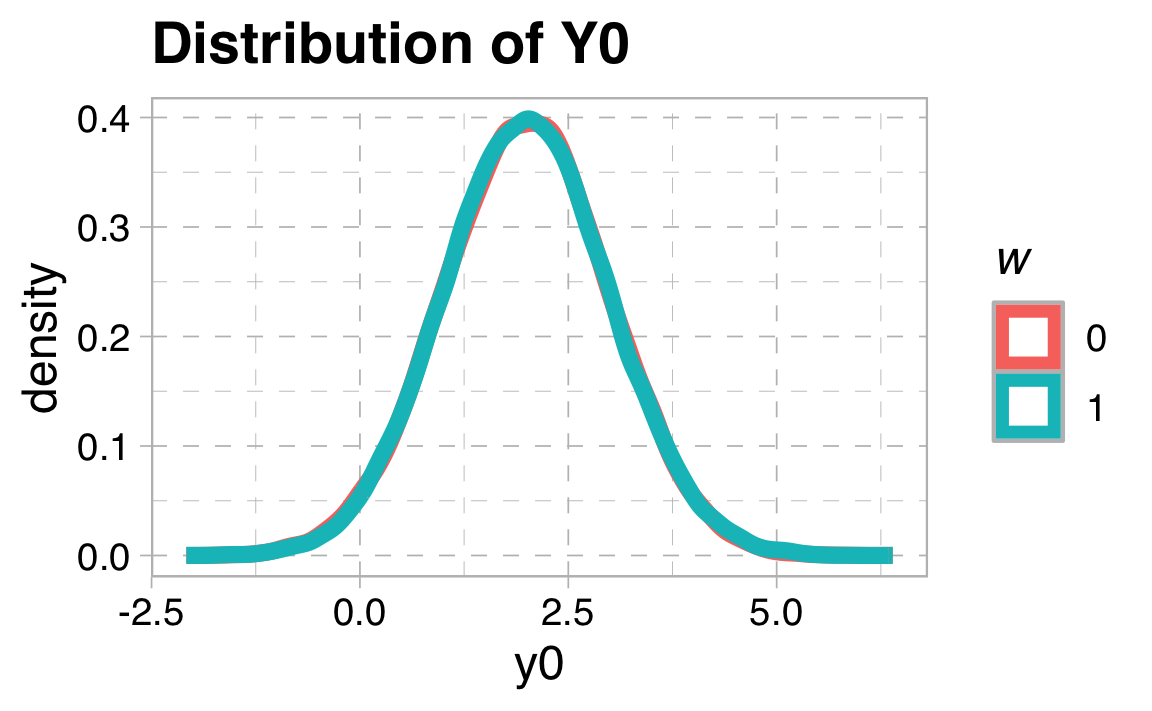
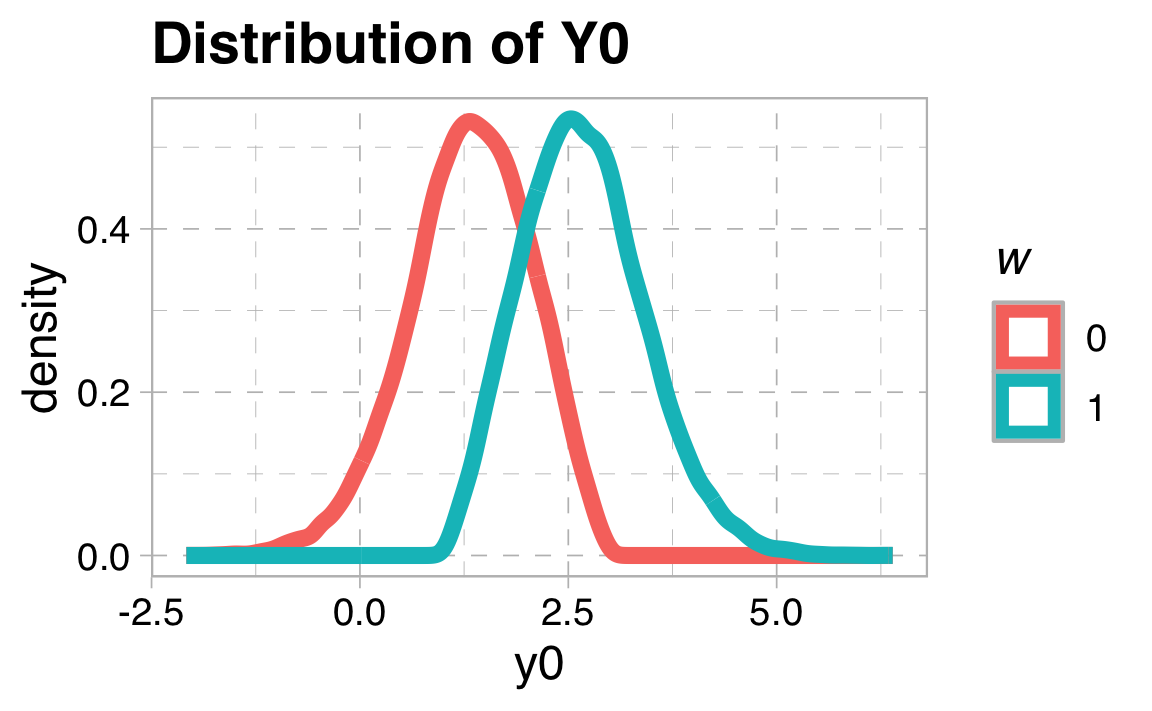
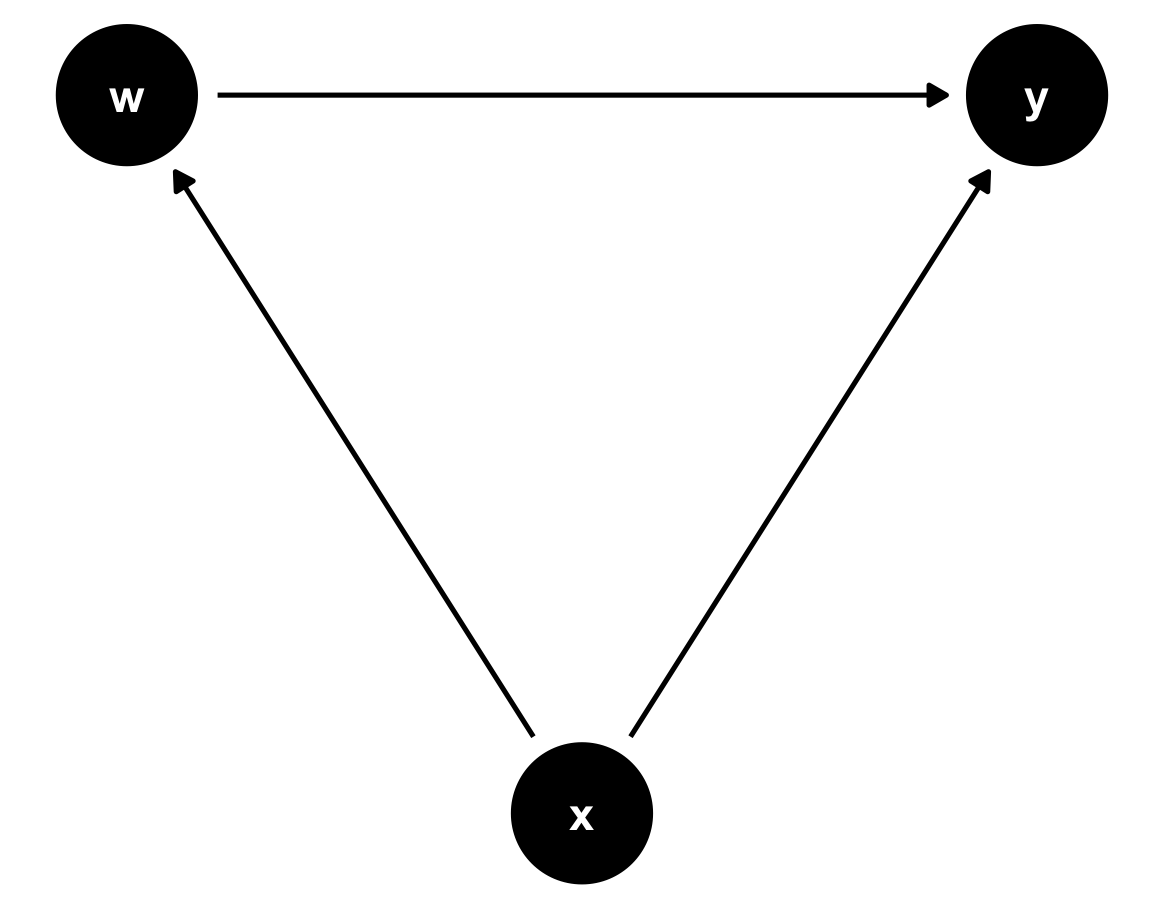
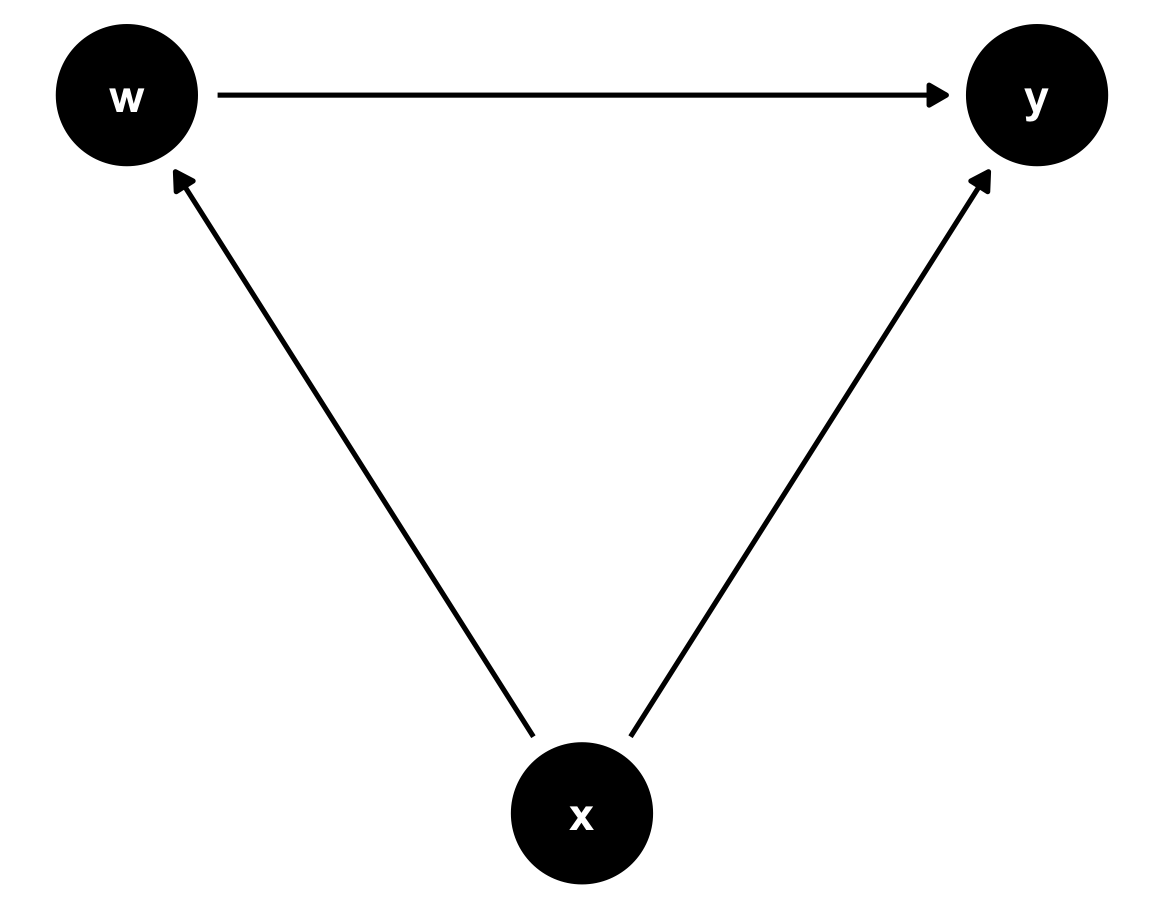
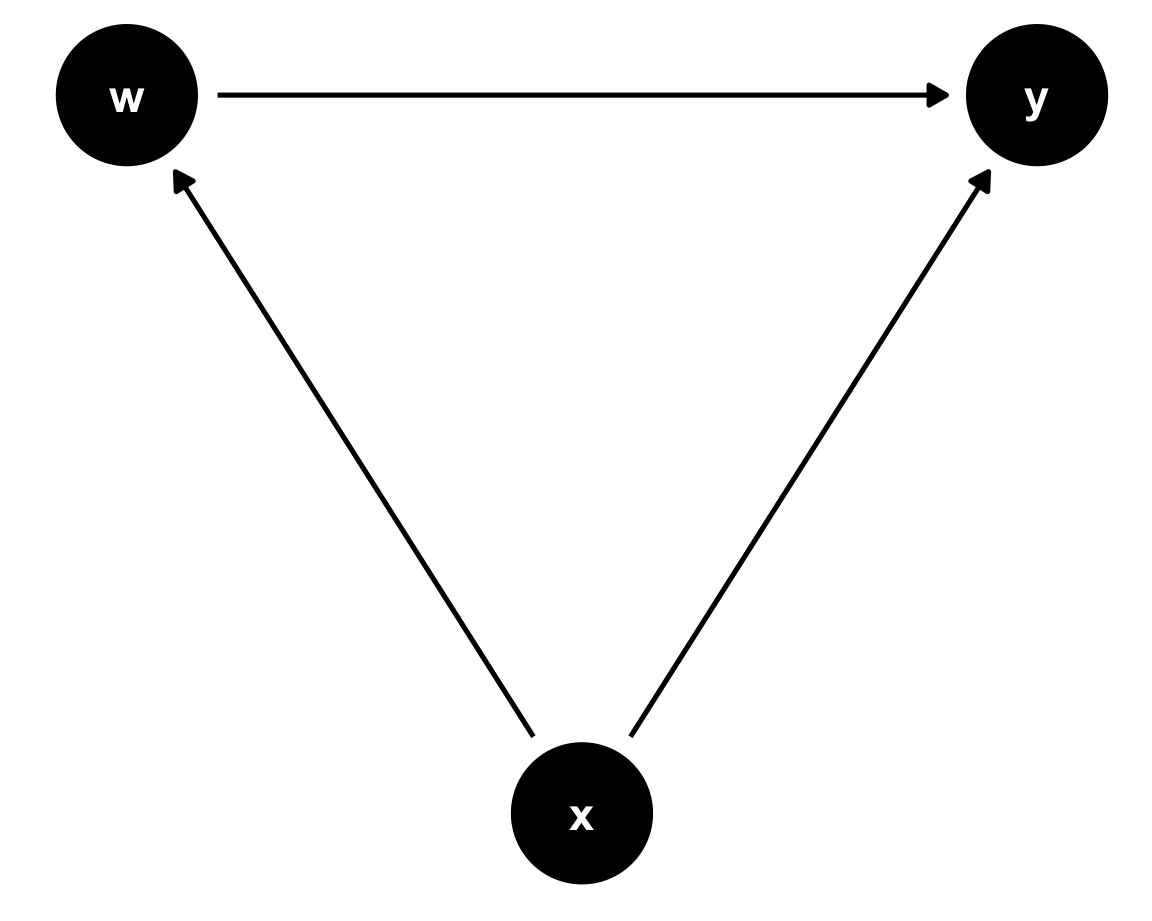
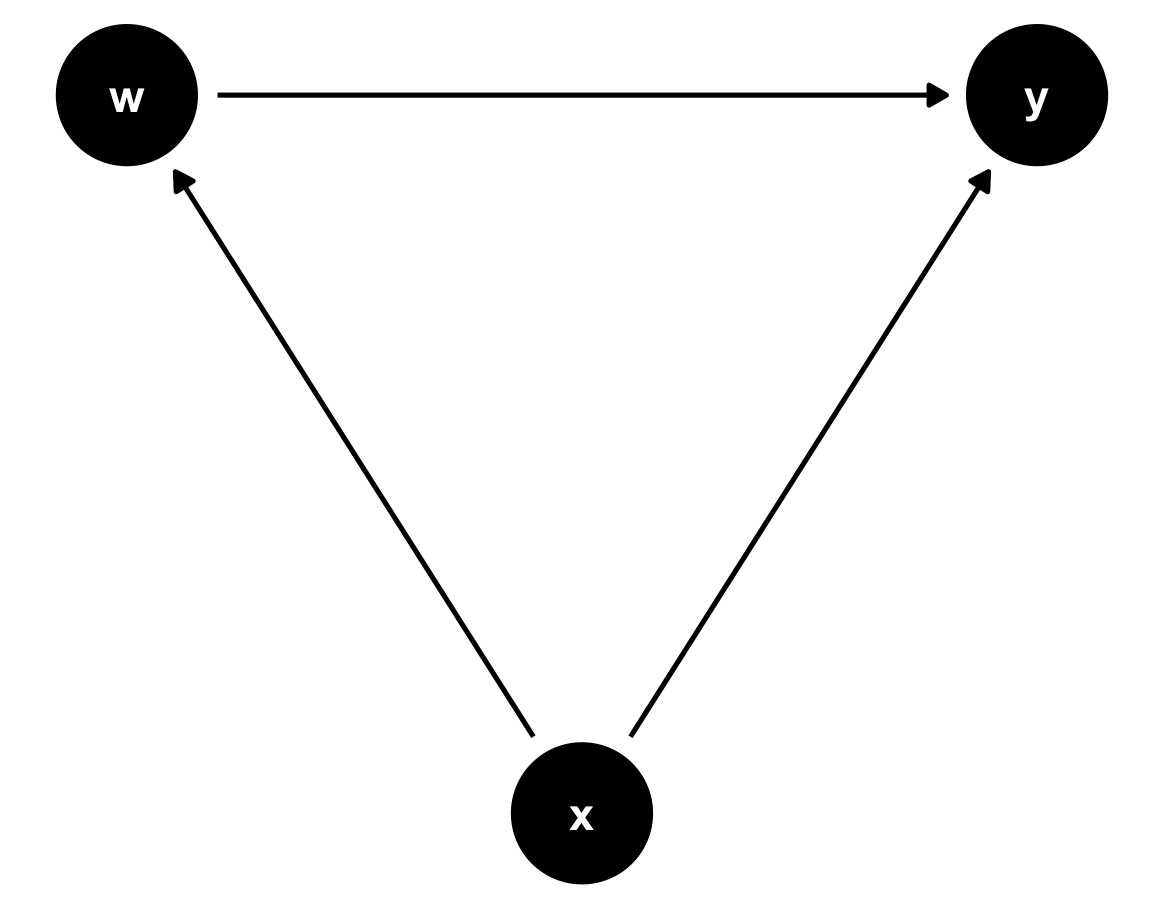
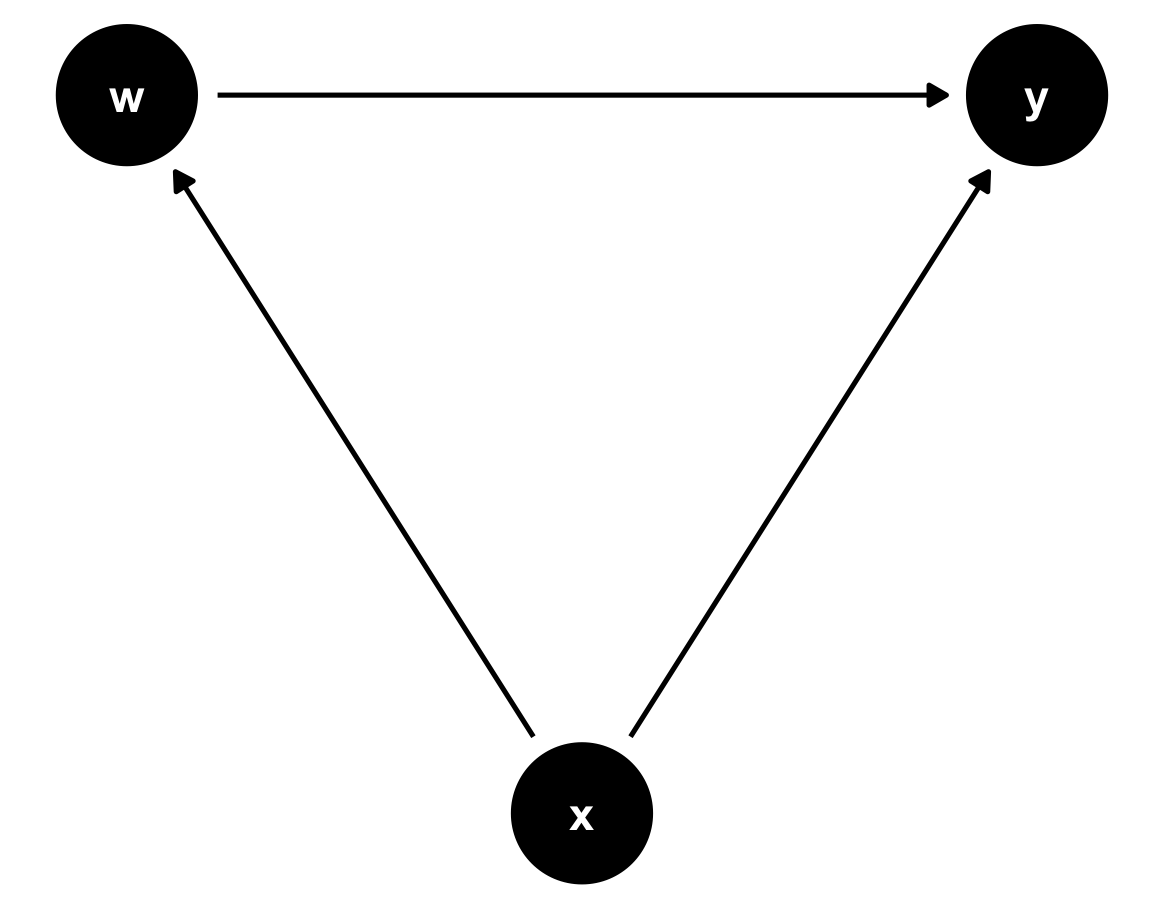
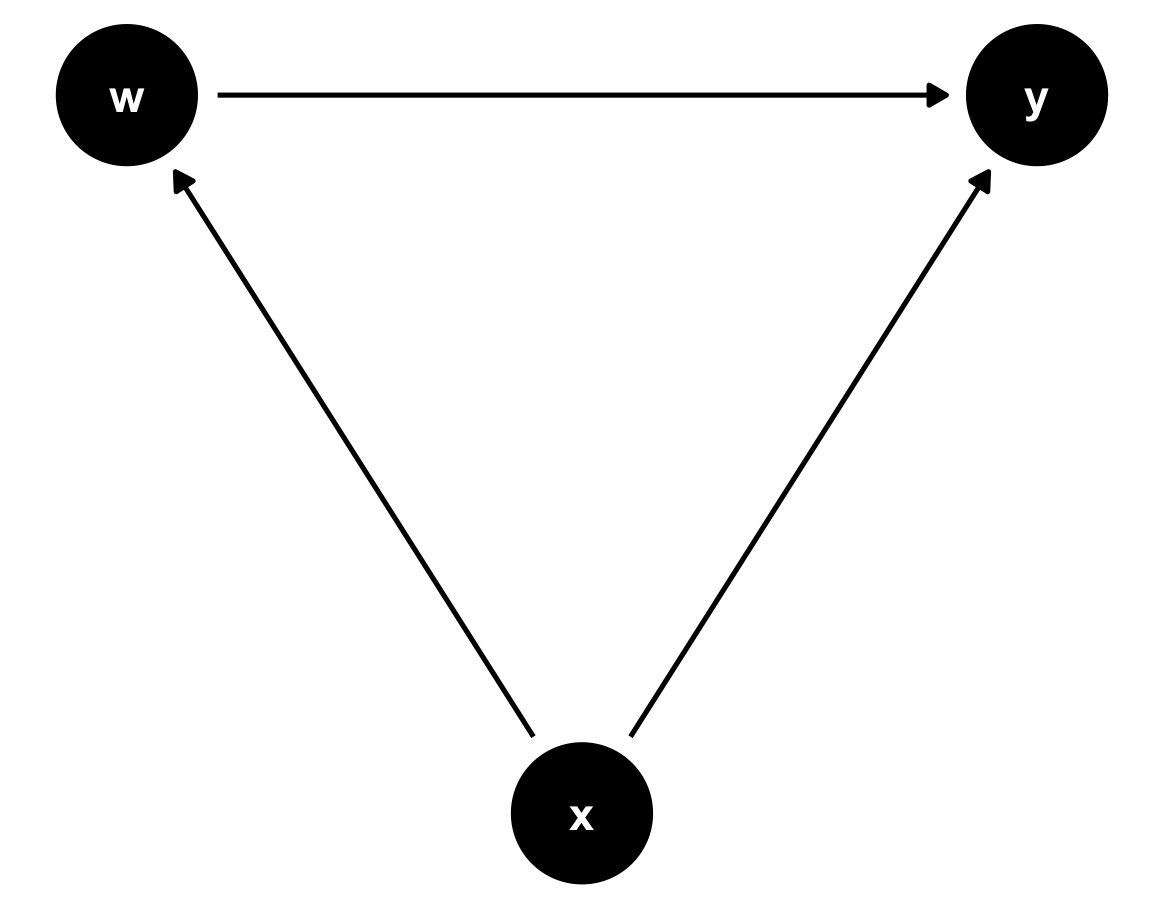
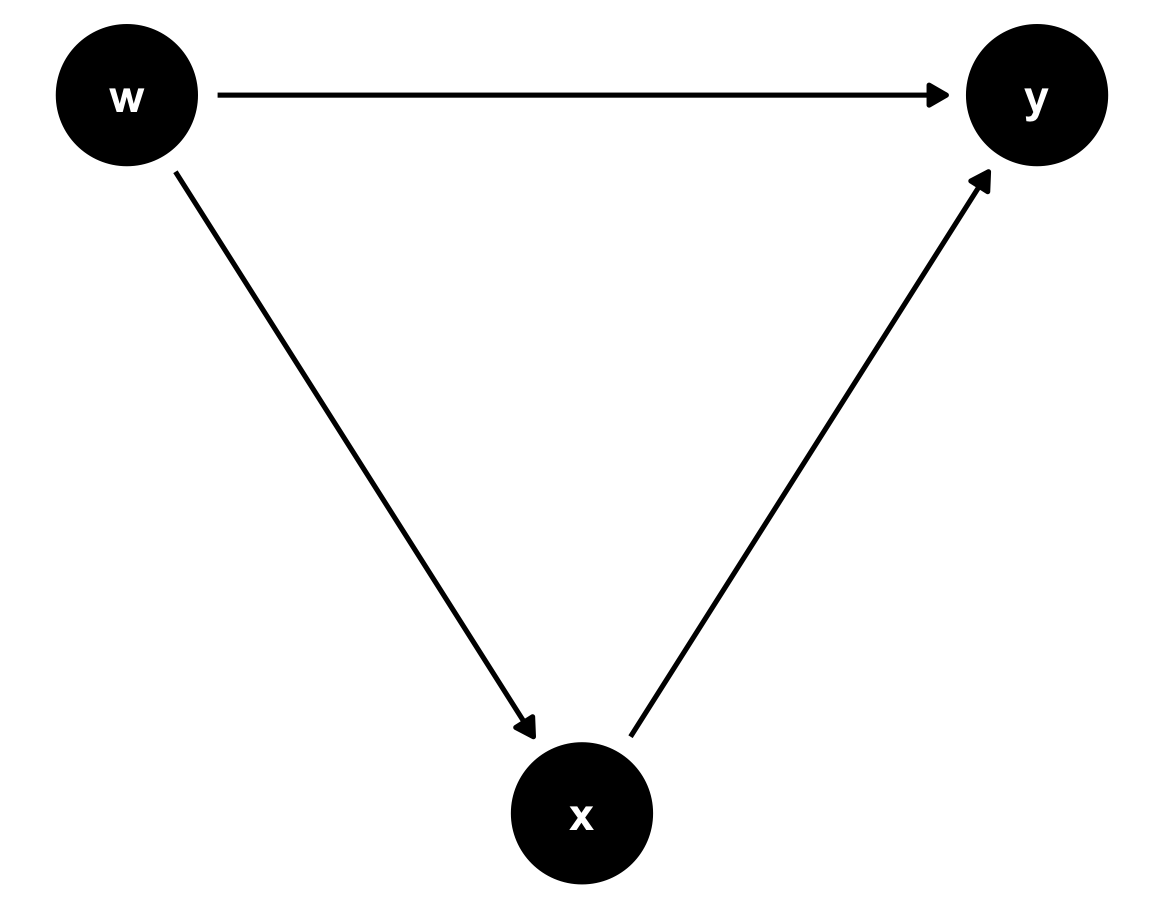
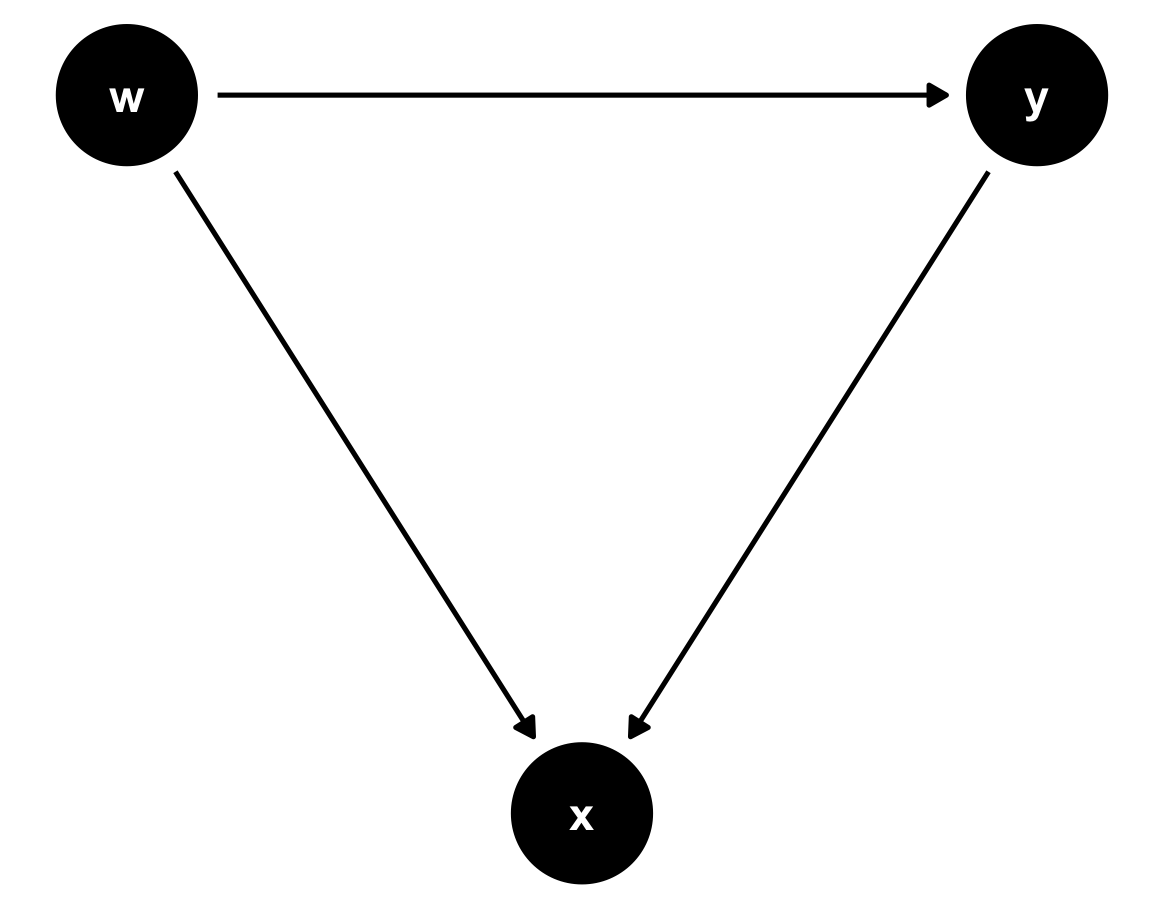
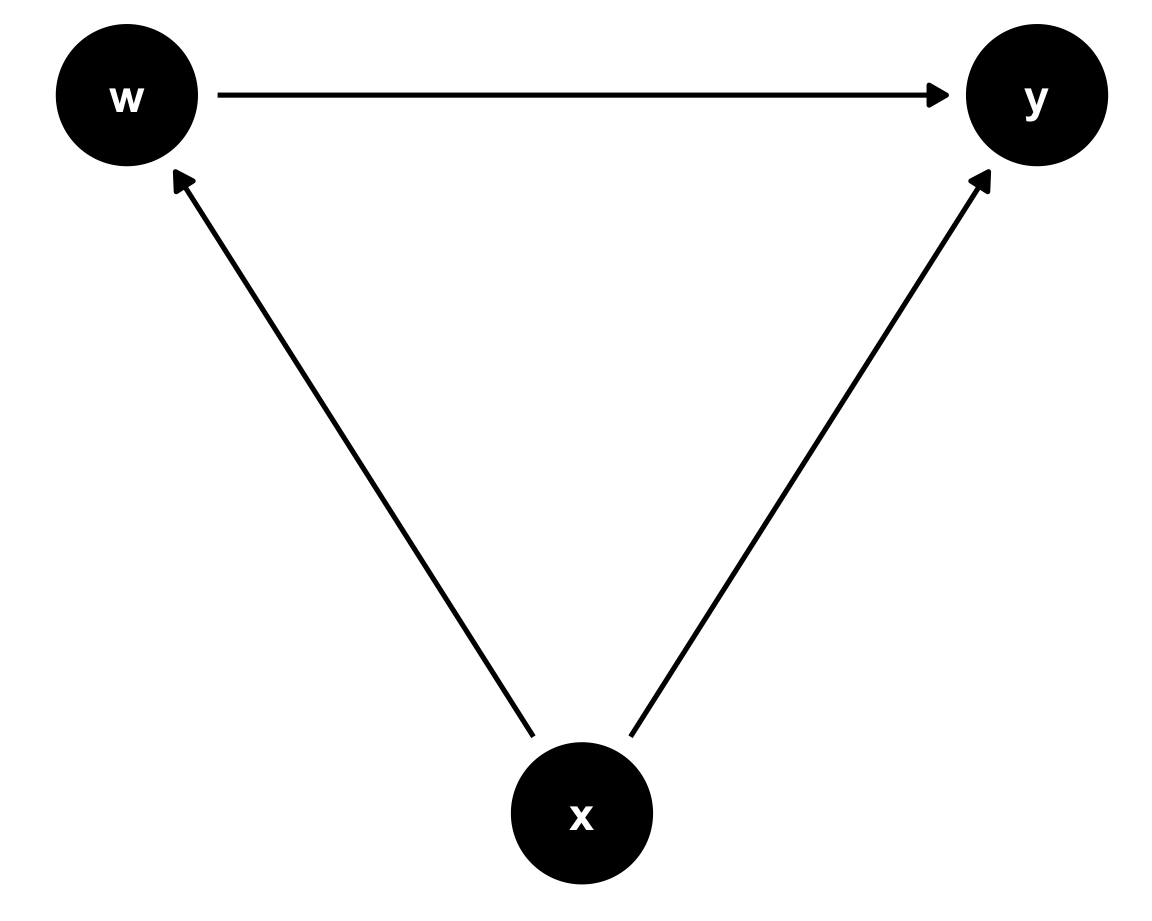
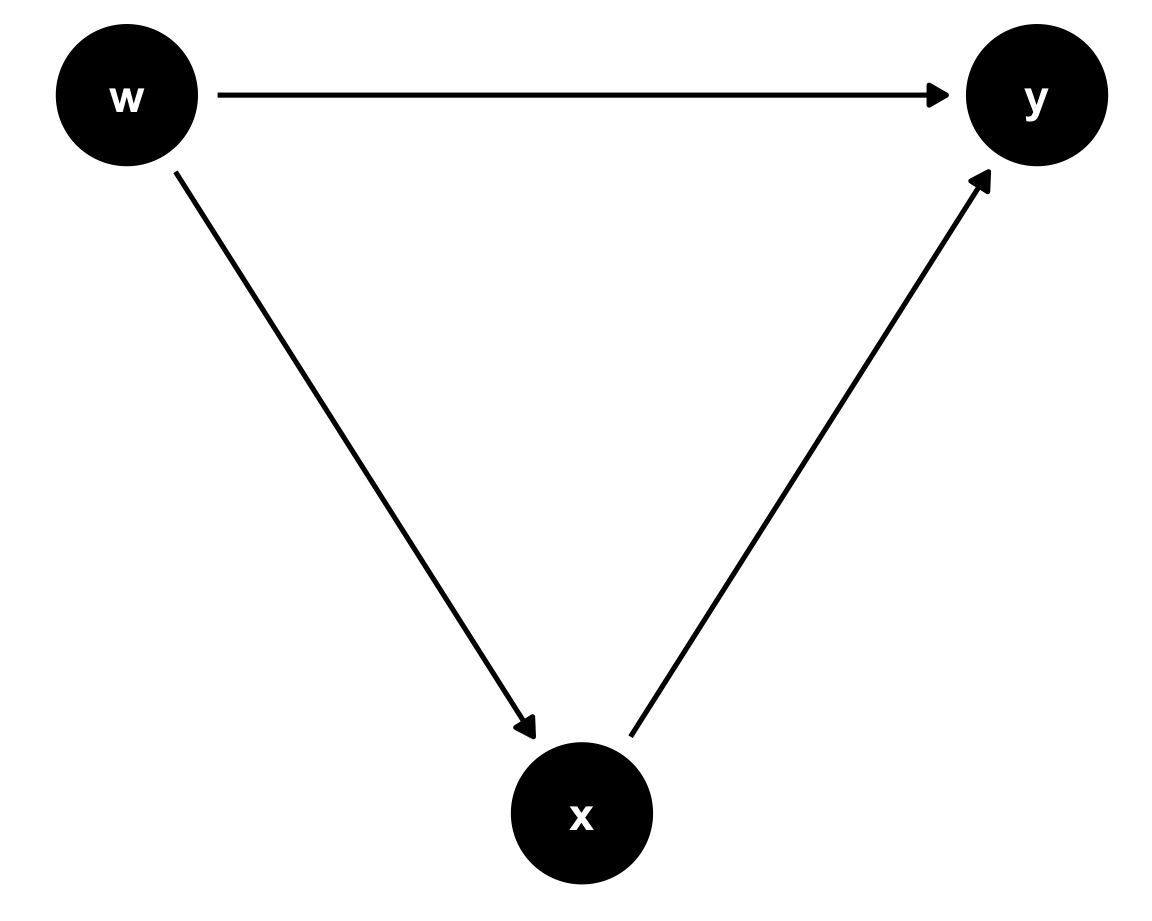
data <- data.frame(eta=rnorm(100000,0,1)) %>%
mutate(y0 = 2 + eta, y1 = y0 + 5,
treat_eff = y1 - y0)
sumtable(data, summ=c('notNA(x)','mean(x)','sd(x)'),
summ.names = c('N', 'Mean', 'SD')) | Variable | N | Mean | SD |
|---|---|---|---|
| eta | 100000 | -0.0012 | 1 |
| y0 | 100000 | 2 | 1 |
| y1 | 100000 | 7 | 1 |
| treat_eff | 100000 | 5 | 0.00000000000000021 |